- Messages
- 2,206
- Reaction score
- 2,824
- Points
- 273
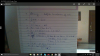
Knowing that u have idea about rules of differentiation. You might have reached to this step :
(i)
dy/dx = -1/[(1 + x)^(3/2).(1 - x)^(1/2)]
Then split dy/dx = (1 + x)^(3/2).(1 - x)^(1/2)
you will obtain result similar to this : (1+x)(1+x)^(1/2).(1-x)^(1/2)
We know that,
(1+x)^(1/2).(1-x)^(1/2) = (1 - x^2)^(1/2)
So now dy/dx = -1/[(1 + x)^(3/2).(1 - x)^(1/2)] = -1 / (1+x).(1 - x^2)^(1/2)
Normal to it is -ve reciprocal of it = (1+x).(1 - x^2)^(1/2)
(ii)
Take y = (1+x).(1 - x^2)^(1/2)
differentiate it.
equate it to zero
obtain x = 1/2