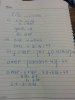- Messages
- 56
- Reaction score
- 9
- Points
- 8
c

an u plz sketch the raph for his 7 marks !!!!It's not too bad as long as you understand that the v/t graph is the graph of the gradient of s/t and remember a few cases.
constant velocity is a straight diagonal line for displacement
straight diagonal line for velocity is increasing gradient graph for displacement
curved graph for velocity is increasing gradient at an increasing/decreasing rate for displacement, depending on the curve in the v/t graph
Because we are doing definite integration. The c cancels out.
There is no 'right' or 'wrong' direction. Positive can be any direction as long as you show motion in the opposite direction as negative.