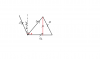- Messages
- 1,660
- Reaction score
- 11,026
- Points
- 523
R^2=P^2+Q^2+2PQCOS thetaAsslamu Alikm waRahmatullahi Wa Barakatoho
...Can anyone show how to solve this question...?
The answer is
106.3 is the angle
and component bit is 7.2N
u will get the angle
i have prblm in the 2nd 1.like the ans would be 10+10 costheta.but y 10 iis added here.they told to find the vector in the direction of OA